Vanishing Point – some surprising features

Report · Jan 25, 2019

In this thread

the question arose how to put square tiles on a floor which is part of the perspective image of a room.

The 3D-room is called "scene", the perspective image simply "image".

"Dave" gave some very useful advice how to apply Photoshop's mode Vanishing Point (VP),

a) for constructing grids,

b) for generating images of orthogonal planes in the scene,

both by Photoshop automatisms.

I'm going now to analyze these automatisms.

a) The task can be solved if the grid cells are images of quadratic tiles in the scene (not

necessarily material ones).

b) Absolutely equivalent would be the calculation of the scene aspect ratio of a rectangle,

which is given by its image quadrilateral. Is it possible to find the true aspect ratio (not the

scale) of a rectangle, when we know its image?

Image 9 shows the view of a cube (and a cone on top) with near vanishing points.

The VP grid is applied to the front face. The grid size is adjusted for integer grid cells.

We have 4 in x-direction and 4 in z-direction. The grid cells are images of square tiles,

a expected (or hoped).

By Ctrl+ drag of the center handle at the right edge the yz-grid is generated. The result looks

good, but it's not entirely correct: we have 5 cells in y direction and 4 in z-direction.

The grid is well aligned.

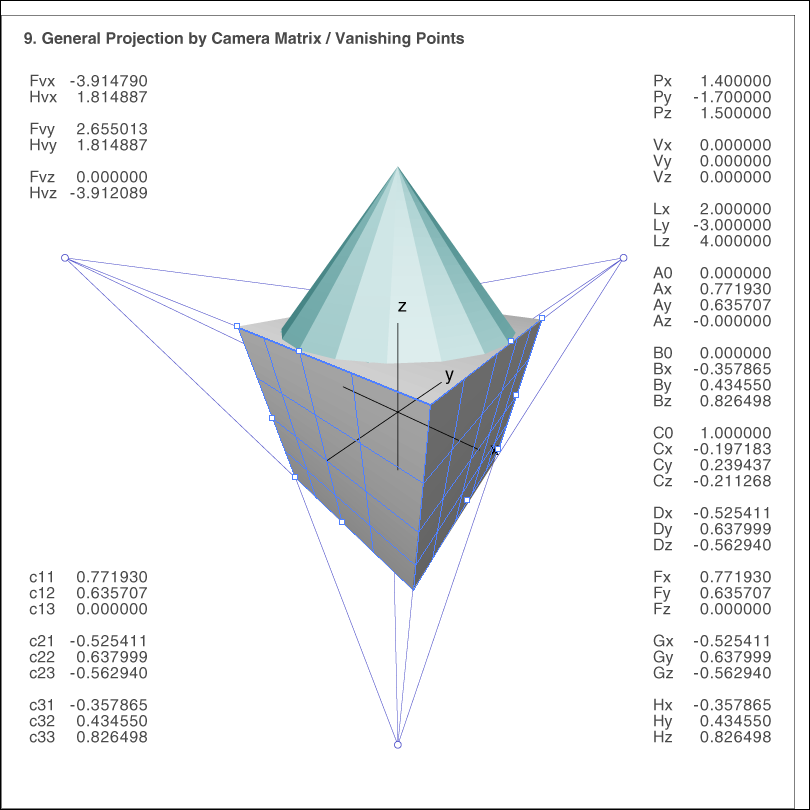
Image 1 below shows the view of a cube with far vanishing points (but not at infinity).

The grid is almost correct, grid cells represent quadratic tiles, but the first column on the right face

is too small.

Image 5 shows the cube with rectified verticals, as we do it by showing a house which is not too high.

The grid is very wrong. We have 8 cells in x-direction and 4 in z-direction. The generation the yz-grid

by Ctrl+drag fails entirely.

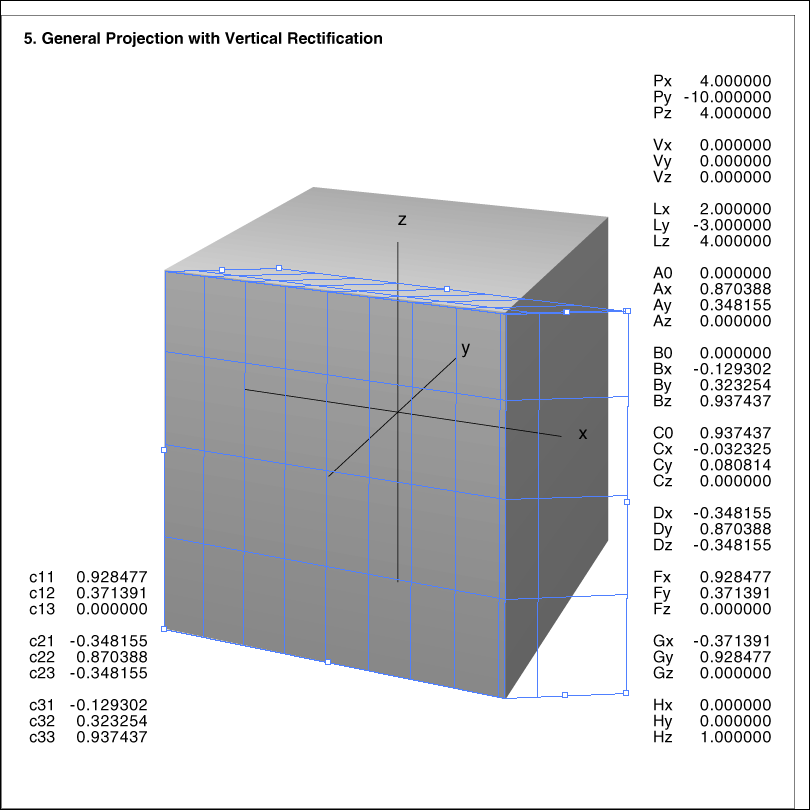
Image 6-red shows an isometric projection. Especially we have 3 pairs of parallel faces in the image.

Generating the front grid fails. This is indicated by the red quadrilateral.

Note: parallel projections are special cases of perspective projections (see [2]).

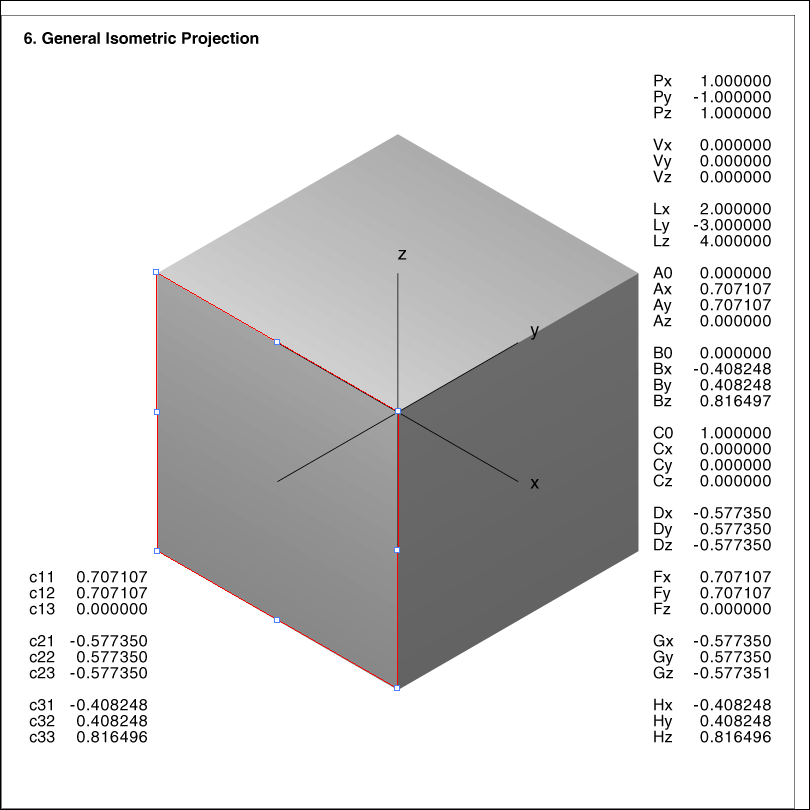
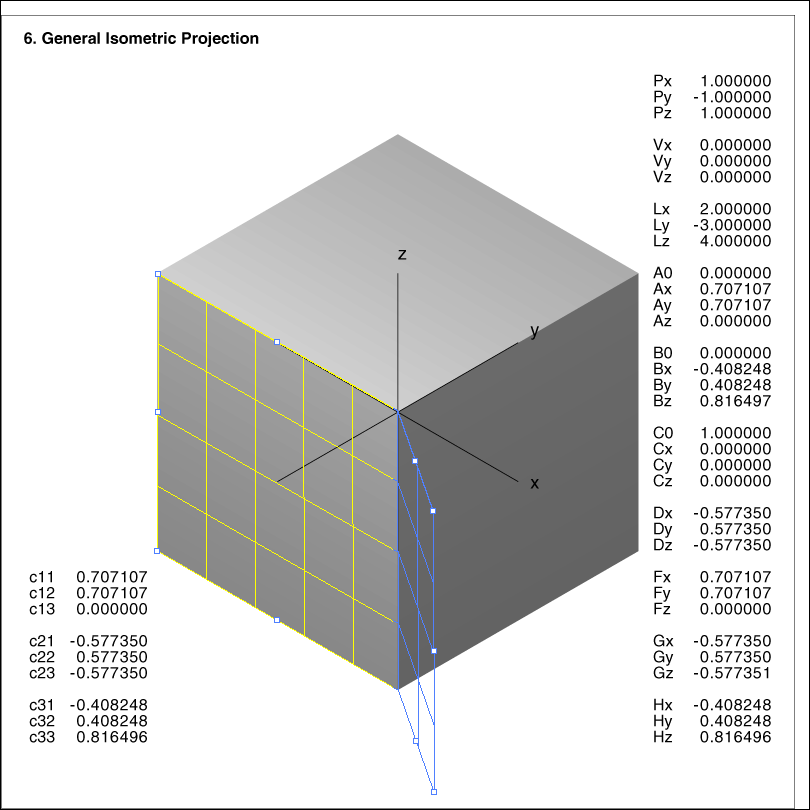
Image 6-yellow shows again the same isometric cube, now with a little fiddling of the control points.

The grid looks reasonable (sometimes it's wrong), but the generation of the yz-plane fails terribly.

The numerical problem is here announced by the yellow color.

We can do many further tests. My result, as already found about 2001, is this:

The aspect ratio of a scene rectangle, which appears as a general quadrilateral by perspective mapping

in an image, can be calculated, if the quadrilateral doesn't have one or two pairs of parallel edges.

Then, the calculation is impossible – if the quadrilateral is either a trapezoid or a rectangle. The calculation

is uncertain, if the quadrilateral is almost such a shape. The disappointing thing about is: the more regular

the shape, the nearer is the mathematical problem to a singularity.

The images of the cube can be found here (2004):

I don't blame Photoshop. VP reasonably applied, is a useful tool, but there are limitations.

Regarding the original task, the equal scale for the tiles of the floor should be checked by other means,

if this (in)accuracy matters.

Best regards --Gernot Hoffmann