Skip to main content
Bicky Perdana
Bicky Perdana
Participating Frequently
April 15, 2023
Answered

Create News Ticker in XD

  • April 15, 2023
  • 2 replies
  • 3526 views

Hello, Masters! It's my first week exploring Adobe XD. And I wanna create a running text (News Ticker) that loops several information (looping forever like gif). That doesn't need any trigger to play. Is it possible in XD now?

I saw some apps that have this feature (News Ticker), but been exploring google how to create one with XD, come empty handed. I attach a video recording of the application that have News Ticker running inside. Thank you so much for your help.

    This topic has been closed for replies.
    Correct answer Spas K.

    Lottie is an animation plugin / format. You can read more about it here. You can use After Effects to create an animation, and export it to a .json file using a plugin called bodymovin. Instead of .gif and video formats, lottie uses javascript to animate vector shapes.

     

    The important thing is, Adobe Xd has support for these lottie files, so you can import one of those animations and use them inside of Xd. The method here is not really concerned with the lottie file itself - that's why we don't care what the contents of the it are. We just use an empty lottie file with the length of 1 frame.

     

    Lottie files have a timeline similar to video, and Xd has an action that can be triggered when the playback of the lottie animation stops. This way we are able to tell Xd "When the lottie animation stops playing, switch to another state or artboard".

     

    So as you've noticed, on the lottie-switch we have 2 different interactions.

     

    The first one is "Time", and is triggered after a certain interval of time after the page / component state is opened. So we tell Xd: After 1 second delay > Start the playback of the lottie animation (the Action is Lottie Playback / Play).

     

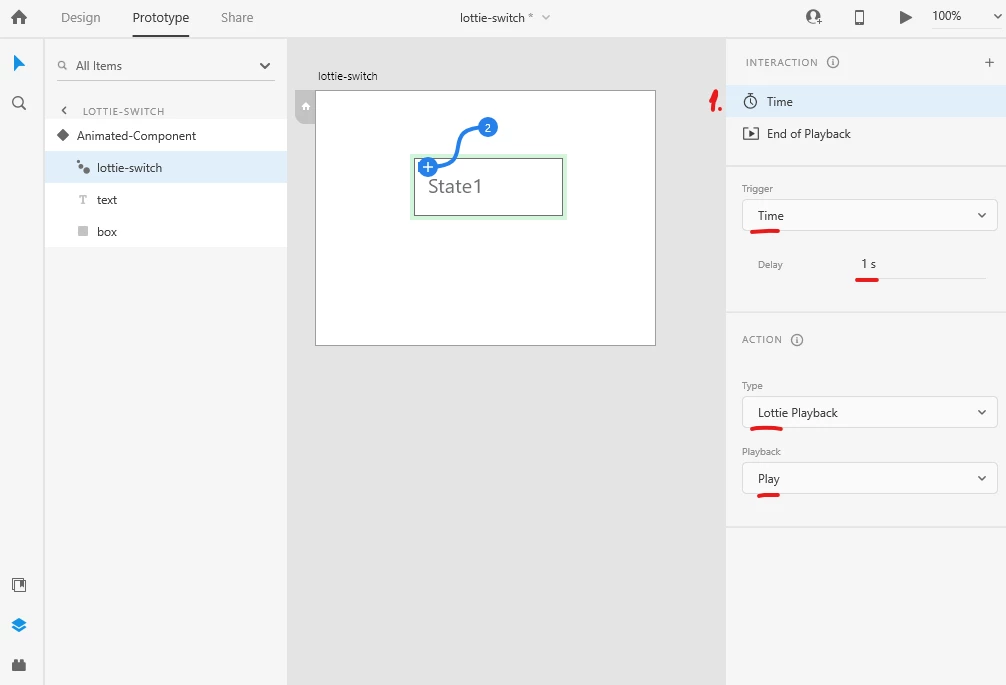
    The second interaction is "End of Playback", which means it will trigger when the Lottie animation stops playing. Because our lottie file is empty and is only 1 frame long, it triggers instantly. Now we tell Xd "when the lottie animation stops playing, auto-animate to State 2 of the component".

     

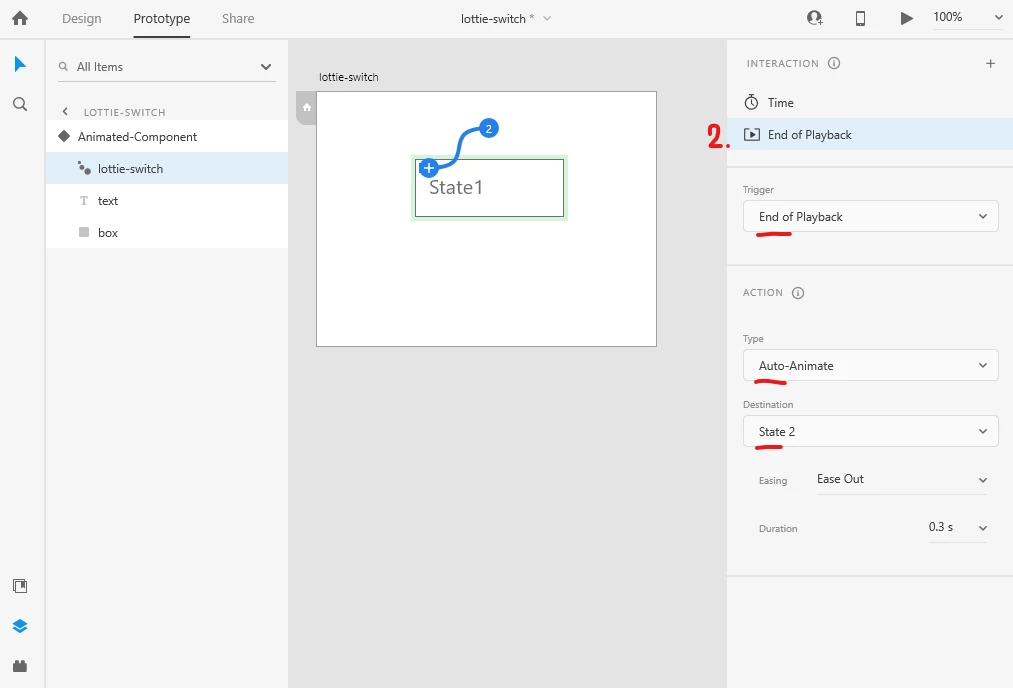
    This is the important part we need the lottie file for, because Xd doesn't allow us to switch to a different state with a Time trigger regularly, but it does when we use the lottie file.

     

    In short:

    1. Delay of 1 second (Time interaction)
    2. Lottie plays for 1 frame
    3. End of Playback switches to a different state

     

    Now in State 2 of the component, we have the same lottie-switch, but at its "End of Playback", it switches to State 3. And in State 3, we have the same switch which points back to Default State. And the whole thing loops every second, because that's what we pointed as our Delay in the Time interaction.

     

    2 replies

    Spas K.
    Community Expert
    Spas K.Community Expert
    Community Expert
    April 15, 2023

    Hi Bicky. In addition to the solution Ares proposed, there's a way to do it using component states, so it can loop inside a component on a single artboard. You will have to make a few states using auto-animate a get a bit creative with how you position your text within the component & mask, so you can get this rolling effect.

     

    Since Xd doesn't support a time trigger for switching component states, there's a little hack using an empty lottie file to trigger the transitions. You can check it out in my reply in this thread.

     

    You could also create your own video file or lottie animation in After Effects with the elements for the news ticker and insert it into Xd. That will probably be the easiest way if you know your way around After Effects & are willing to look into animating with Lottie, since you won't have to play around with Xd's fragile components which are tricky to set up for such complex cases and rarely work without issues.

      Bicky Perdana
      Bicky PerdanaAuthor
      Participating Frequently
      April 23, 2023

      Hello, thank you for your reply. I have hunch this answer is closer to what I'm looking for.  But I don't understand this "lottie" thing (first time to hear it actually). Been googling this "lottie", but I still don't get it.

      Find a lottie online which have the thing. But I have no idea how to use it.
      https://lottiefiles.com/lottie-to-gif/convert?url=https%3A%2F%2Fassets9.lottiefiles.com%2Fpackages%2Flf20_qxd4ey0x.json&bg_color=ffffff

      Please help further, thank you so much.

      Ares Hovhannesyan
      Community Expert
      Ares HovhannesyanCommunity Expert
      Community Expert
      April 15, 2023

      I think you need something like this

      How to create loading text animations in Adobe XD - YouTube

      For creating some simple animation try this

      Creating a running text in Adobe XD, follow these steps:

      - Select the Text tool from the toolbar or press T on your keyboard.
      - Click and drag on the canvas to create a text area. You can adjust the size and shape of the text area by dragging the handles on the corners and edges.
      - Type or paste your text in the text area. You can use the Property Inspector on the right to change the font, size, color, alignment, and other text properties.
      - To create a running text effect, you need to animate the text area using Auto-Animate. To do this, you need to create at least two artboards with different states of the text area.
      - On the first artboard, position the text area where you want it to start. You can also adjust the opacity of the text area to make it fade in or out.
      - On the second artboard, position the text area where you want it to end. You can also adjust the opacity of the text area to make it fade in or out.
      - Make sure that both artboards have the same size and that the text areas have the same name and properties. You can use the Align and Distribute tools to align them precisely.
      - Select both artboards and click on Prototype at the top of the screen. This will switch to the Prototype mode where you can create interactions between artboards.
      - Click on the first artboard and drag a blue wire to the second artboard. This will create a trigger for the animation. You can choose from different types of triggers such as Tap, Drag, Time, Voice, Keyboard, Gamepad, or Hover.
      - In this case, we will use a Time trigger to make the animation start automatically. To do this, select Time from the drop-down menu and set a delay for how long you want to wait before starting the animation. You can also set an easing and a duration for how fast or slow you want the animation to be.
      - To make the animation loop, you need to create another wire from the second artboard back to the first artboard. Select the second artboard and drag a blue wire to the first artboard. Choose Time as the trigger again and set a delay for how long you want to wait before repeating the animation. You can also set an easing and a duration for how fast or slow you want the animation to be.
      - To preview your animation, click on Preview at the top of the screen. This will open a window where you can see how your animation looks and behaves. You can also use your keyboard or mouse to interact with your prototype if you have other triggers besides Time.

        Bicky Perdana
        Bicky PerdanaAuthor
        Participating Frequently
        April 23, 2023

        Thank you for your reply. Actually, this is not what i'm looking for.

        But these really are some interesting trick. I'm new to XD, so I'll save it for later.

        Terms & ConditionsAccessibility statement
        Using the community Terms of use Privacy Cookie preferences Do not sell or share my personal information ad choicesAdChoices