Skip to main content
A
Alp_Er_Tunga
Participating Frequently
September 10, 2014
Question

Visual representations of color spaces

  • September 10, 2014
  • 1 reply
  • 27673 views

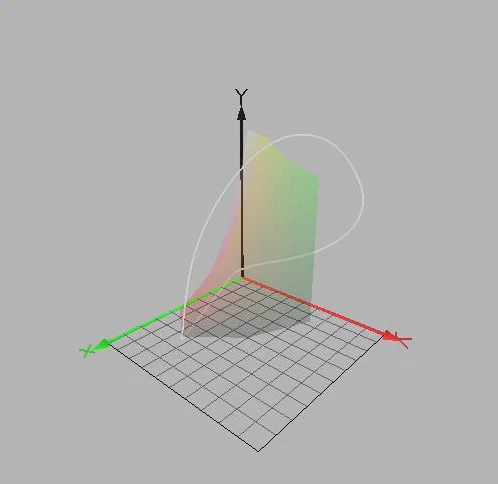
I copied these diagrams from the program called Color Space ...

Can be downloaded from here: COULEUR.ORG

I think that it draws spectral locus on xyY by just plotting matching x, y and Y values for every interval of monochromatic lights on the spectrum ... just like we draw the locus line in XYZ by plotting matching tristimulus values X, Y and Z.

Because the underlying data for the most saturated colors human can see is CIE XYZ color matching functions, I think that we can draw the line of spectral locus in every model originated from CIE XYZ by just making necessary transformations to the XYZ tristimulus values for the intended model.

3D representation of the entire human gamut is more tricky, I think. I will ask about it, after getting your confirmation about the spectrum locus.

    This topic has been closed for replies.

    1 reply

    G
    G_Hoffmann
    Inspiring
    September 11, 2014

    Without further explanations these graphics are rather dubious, in my humble opinion.

    http://docs-hoffmann.de/ciexyz29082000.pdf

    On p.8 we can see, how XYZ is mapped onto the plane X+Y+Z=1 as coordinate system xy
    by a perspective projection:

    The original Y-axis is not orthogonal to the plane xy, therefore the quoted diagrams
    are not correct. It's of course possible to construct a kind of substitution Y* orthogonally
    to xy.

    As long as we are talking about unrelated colors, like an arbitrary set of spectral light
    sources with arbitrary radiant powers, the human gamut in XYZ is indeed a cone,
    which has its vertex at X=Y=Z=0 and which intersects the plane X+Y+Z=1 by this
    horseshoe curve (plus purple line for mixtures of extreme spectral red and blue).

    About power:

    http://en.wikipedia.org/wiki/Radiant_flux
    "radiometric power", correctly: radiant power or radiant flux

    The situation becomes different under certain circumstances where the unlimited cone is
    replaced by a finite volume or by finite curves on this cone:

    1) The radiant power of the spectral light sources is limited and equal, e.g. 1 Watt.
        The curve on the cone shows the spectral loci. In Wyszecki&Stiles in chapter 3.3.3
        in Fig. 4(3.3.3) exactly this situation is illustrated: we can see the cone, the horseshoe and

        the spectral locus on the cone.
        As already mentioned, this issue has been further evaluated by Jim Worthey ("amplitude
        not left out" and illustrated by me and of course by himself  (see references):
        http://docs-hoffmann.de/jimcolor12062004.pdf

    2) The volume of Optimal surface colors, concept by Roesch, as already explained.
        Fig. 5(3.7) in W&S shows Y orthogonally over xy, which is not correct, but we understand
        the meaning. This 'wet sack' has on top Y=100, which is the luminance of the illuminant.

    3) A color space is a subset of a finite gamut volume in XYZ. There is always a white point and
       nothing can become brighter than the white point. An RGB space is represented in XYZ by an
       affine distorted cube. Mapping to xy delivers a triangle, but here we can see, what happens

       if the "amplitude is not left out":
       http://docs-hoffmann.de/ciegamut16012003.pdf
       The sections Y=const. with the dark sides of the cube appear still as triangles, but the sections

       with the bright sides by other polygons (p.12 for sRGB).

       A threedimensional graphic would be possible, Y over xy.

    Best regards --Gernot Hoffmann

    A
    Alp_Er_TungaAuthor
    Participating Frequently
    September 13, 2014

    I would like to ask some basic questions.

    The following diagram is the Adobe RGB appearance in xyY (Color Think Pro):

    1. Does any white point conversion visually mean shifting the place of the top vertex in the graph ... and recalculating the other colors according to this shifting vertex?

    2. Is the white point normal to equi-energy stimulus ... I mean an orthogonal line from the white point to the xy plane intersects the xy plane on the equi-energy point?

    3. Is it possible to show the Planckian locus in xyY space? 

    G
    G_Hoffmann
    Inspiring
    September 16, 2014

    Sorry for the delay, I've been travelling and pondering over your ColorThink diagram.

    Here we see a diagram 3D-xyY according to Adobe:

    http://dba.med.sc.edu/price/irf/Adobe_tg/models/ciexyz.html

    Note that the base of this object is flat, not like a pyramide in the ColorThink diagram

    (black lines).

    Here we see my diagram xyY in 2D-xy with contours Y=const:
    http://docs-hoffmann.de/ciegamut16012003.pdf
    p.2 + p.12

    Both representations are equivalent.

    Now I'm trying to interprete the ColorThink graphics:

    The appearance of an RGB color cube in  XYZ, which is now called
    XYZ-cube, is shown here:
    http://docs-hoffmann.de/ciexyz29082000.pdf
    p.5

    Three base vectors R,G,B represent the three 'dark edges' of the XYZ-cube.

    The other 9 edges are formed by linear combinations of the base vectors

    like C=rR+gG+bB with special factors r,g,b,  fixed 0 or 1 and in the range (0...1):
    For instance
    C=1R+(0...1)G is the edge from red to orange.

    The XYZ-cube is an affine transformed regular cube. Straight edges of the
    regular cube are mapped to straight edges of the XYZ-cube.

    What we see in the ColorThink graphics is a 3D-color space which seems
    to be a perspective transform of the XYZ-cube, 'erected' over the chromaticity
    plane xy with Y as third coordinate. But this object does not have straight edges,
    therefore it's not a perspectively mapped XYZ-cube, because perspective
    mapping (like affine mapping) would have preserved straight edges. What is it?

    3D-CIELab over xy? Sorry, I don't know how this object had been generated.   

    About the other questions:

    A white point conversion is generated by varying the lengths of the base vectors

    or the directions or both.

    The base vectors appear in xy as 'primaries' (the nomenclature may vary).

    If only the lengths of the base vectors are changed (and not their direction), then

    the primaries in xy are the same.

    The new white point in XYZ is achieved by Wn=Rn+Gn+Bn. If we apply previously

    used factors r,g,b, the all colors are shifted automatically for the new white point.

    A color with flat spectrum (in the relevant  range) is called 'Equal Energy Stimulus'.

    Such a spectrum does not exist for any natural or technical light. The color in XYZ

    is the Equal Enery White point, which ist mapped to xy by a straight line through

    this point and the point X=Y=Z=0, intersecting the plane X+Y+Z=1 in xe=ye=1/3.

    The Planckian locus is a curve of chromaticities. It can be shown exactly and

    by approximation for different 'correlated color temperatures' in xy:

    http://docs-hoffmann.de/coltemp18102003.pdf

    Obviously any arbitrary light source or illuminant doesn't have an assigned

    white point in XYZ at Y=100 (Y is arbitrary). Therefore a diagramm Y over xy

    wouldn't make any sense here, in my opinion. A good argument for the introduction

    of the chromaticity diagram!

    Now I hope, these explanations are more or less correct. I don't know how to edit

    already posted contributions, therefore some errors might have been left.

    Best regards --Gernot Hoffmann 

    Terms & ConditionsAccessibility statement
    Using the community Terms of use Privacy Cookie preferences Do not sell or share my personal information ad choicesAdChoices