Maximum distance across any axis (circumscription)?

[RSDD-gVlSis]

I posted this in general "Illustrator", but I think it might be better suited here.

I'm looking for a way to constrain an object to a size across any axis. For example, a 3" x 4" rectangle has a maximum height (or width) of 4". But it will not fit inside a circle with a 4" diameter. If you rotate the rectangle 45°, it now has a width of 4.9498" and a height of 4.9497". This works fine when the diagonal is obviously the longest measurement.

But what about irregular shapes (the one I'm working with is the outline of a padlock)?

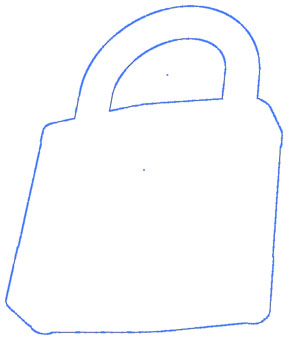
The center point moves depending on the rotation, and some paths have so many points, finding the two furthest from each other is almost impossible. Any good ideas for finding the longest edge-to-edge distance? I figure once I can do that, I can then scale by percentage to the size I'm looking to fit.

Thanks!

[JETalmage · Accepted solution]

First, finding the greatest distance between anchorPoints of a given path via Javascript would be fairly trivial. But AI's Javascript model does not provide a means by which to find the extrema of a curved segment. (And clearly, both ends of the greatest distance across your figure will be on curved segments.) To do that via Javascript, you would have to essentially construct the Bezier math in Javascript--a considerably more ambitious task.

Second, If your belief is that the "longest distance across" an irregular shape will yield the circumcircle (actually, the smallest bounding circle) of that shape, you are mistaken (as was explained in your other thread after your rather smart-aleky response to someone trying to help you).

See your other thread in the Illustrator forum for more explanation.

JET

[MarkWalsh]

One thing you could try, would be rotating the object 360° in steps, checking the height (or width) of the bounds of the object, and getting the largest value. Not 100% accurate, but if you use a small rotation amount (perhaps .5°), it should be pretty close.

[JETalmage]

A pentagon, for one example, would result in five different rotation angles, all yielding the greatest height (or width). Yes, the Javascript could be made to just pick one of those five. Yet even after going through all that, RSDD's purpose would not be served: a circle of that diameter would still not be the circumcircle of the pentagon. It would be too small.

The same would be true of an equilateral triangle: the length of any one side will clearly be the greatest distance between two points on the path; but it will not be the diameter of the triangle's circumcircle.

Moreover, RSDD is trying to find the minimum bounding circle of any irregular polygon. As explained, that cannot be reliably found by merely finding the maximum distance across the object.

JET

[MarkWalsh]

It looks like it does what the OP wants to me:

var docRef = app.activeDocument

var maxWidth

var currentWidth

maxWidth = 0

currentWidth = 0

if (docRef.pageItems.length > 0) {

for (var i = 0 ; i < 360; i++) {

currentWidth = docRef.pageItems[0].width

if (currentWidth > maxWidth) {

maxWidth = currentWidth

}

docRef.pageItems[0].rotate(1)

}

}

alert(maxWidth)

This gives me a diameter for a circle which fits the shape, with several irregular polygons I tested with.

[JETalmage]

Mark,

To see why it doesn't work:

1. Rectangle tool: Draw a vertically-oriented rectangle.

2. Minus Pen tool. Delete the upper right corner anchorPoint. Now you have a right triangle.

3. Run your script. The script will return a measure which is the hypoteneuse of the triangle, and it will circumscribe the triangle when the circle is centered on the hypoteneuse.

But it will NOT circumscribe a triangle with three accute angles:

4. Create the same right triangle, as in steps 1 & 2.

5. White Pointer: select the lower left anchorPoint (the one at the right angle), and drag it leftward, so as to create an accute angle at that point. Do not drag it so that any of its two legs are longer than the former hypoteneuse.

6. Run your script.

You will see that the resulting circle is not large enough to circumscribe the irregular polygon. (Just as demonstrated with RSDD's padlock in my first post.)

JET

[MarkWalsh]

I see now. The irregular shapes that I tested with (including a tracing of the original lock) were apparently not irregular enough, and gave me results that were close enough to appear to work. (Odd, I've never been accused of not being irregular enough before. )

I tried duplicating the shape to get a true circular shape to test the size to see if that would be the answer, but with some shapes, the resulting circular area was larger than the most efficient size.

[JETalmage]

It's the classic geometric problem of finding the smallest bounding circle for a given set of points (or for an irregular polygon). There are algorithms for doing it, but they are not simple. However, even pursuing them for the purpose stated is most likely a fruitless endeavor, because of two problems, one geometrically exacerbating; the other aesthetic:

Remember, the purpose is to find a bounding circle to tightly enclose something drawn in Illustrator--basically, an icon in a tightly-fitting circle.

The goemetric complication is that most attempts at solving the smallest bounding circle assumes a scatter plot of points or corners of an irregular polygon. But in the context of an icon drawn in Illustrator, those methods overlook the fact that the extrema of the shape might just as likely be somewhere along curved Bezier segments as at actual anchorPoints. So a real geometric solution would have to include an algorithm for positioning points at those outlying curve edges. The padlock subject of the original post is just such a case-in-point. The largest diameter of the figure clearly happens to fall somewhere in the middle of curved segments at both ends.

But even if you expend the scripting energy to solve for all that, there still remains a practical consideration that defeats the whole purpose: Suitability of the resulting design. Again, the specific artwork shown is a case-in-point. You can easily approximate the smallest bounding circle for that padlock figure manually in Illustrator, without the need to resort to any scripting or other automation. But after doing so, you'll likely find the result visually unsatisfactory: the padlock will not appear to be centered in the circle. Thus, graphic discernment is going to come into play anyway, and a bounding circle other than the smallest is, more often than not, going to be the most desirable.

Again, boiling the problem down to the simplest figure--a circumscribed triangle--serves to prove that problem as well:

Geometry dictates that for any right triangle circumscribed by its smallest bounding circle, the hypoteneus will be a diameter of the circle. You can demonstrate that by:

1. Draw a circle.

2. Draw one diameter.

3. Select any other point on the circle.

4. Connect the added point to each end of the diameter, and the resulting three lines will always result in a right triangle.

The above exercise clearly results in the right triangle being circumscribed by its smallest bounding circle. But would you call that triangle "centered" in the circle? Certainly not. The right triangle, by necessity, occupies only one half of the circle.

Now move the corner point that forms the right angle a little outboard of the circle. What you are now viewing should clearly demonstrate the rule already explained: that the longest diameter of the original artwork (in this case, the former hypoteneus) cannot be the diameter of even an enclosing circle if any third point of the figure forms an accute angle with the diameter's two ends.

There is, of course, a single minimum bounding circle for this new triangle, but once you find it, you will still see that the triangle is not "centered" in the circle. It will be "better centered" than the former right triangle, but it will never become what anyone would call "visually centered" or "balanced" until you've move that third point around so as to form an equilateral triangle. In other words, among triangles, only an equilateral triangle will ever appear what we would call "centered" in its minimum bounding circle. That problem is even more likely in the far more variable possibilities of irregular polygons, let alone all the many shapes that can be drawn in Illustrator, including those with curved segments defining their extremes.

There is a very simple and practical method for achieving what RSDD wants without resorting to scripting or even simple math. It was explained to him in his first thread on this question in the Illustrator general discussion forum. But he offhandedly dismissed it on the grounds that "it can't be that simple."

JET

[JETalmage]

MarkWalsh wrote:

I see now. The irregular shapes that I tested with (including a tracing of the original lock) were apparently not irregular enough...

It's not that your test shapes were not irregular enough. As pointed out earlier, the method employed by the script will fail to generate a bounding circle even for a pentagon--a perfectly regular polygon.

The script will work for a rectangle. It will not work for an equilateral triangle.

It will work for any regular polygon with an even numbrer of sides, but will work for none with an odd number of sides.

It will work for any irregular polygon in which all of the other vertices make an obtuse or right angle with the two most distant vertices.

It will not work for any irregular polygon which has even one other vertex which makes an accute angle with the two most distant vertices.

JET

[RSDD-gVlSis]

My apologies to JET and the members of the forum for my too quick response to JET's post early in this discussion. I jumped to conclusions and replied out of frustration. I appreciate JET's answers and, after reading through them, I realize that the problem is far more difficult than I initially thought and that, in true application of Occam's Razor, his method is actually the most practical. Thank you, JET, for your input and patience.

RSDD