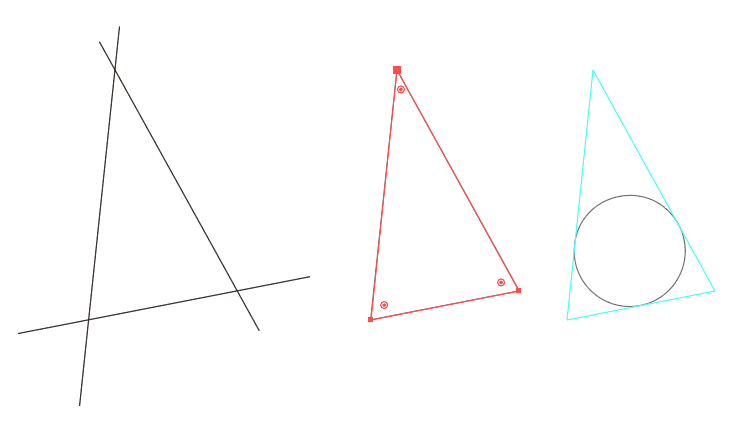Copy link to clipboard
Copied
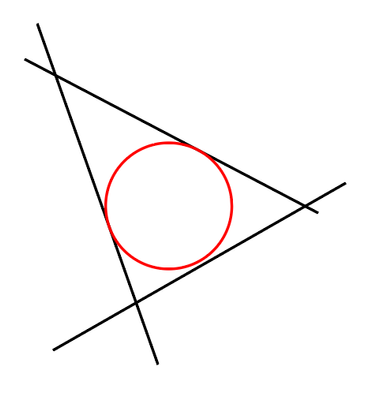
I used Astute Graphics's "Tangent Circle Tool" to make it tangential to two of the three straight lines, but I want it to be tangential to all of the three straight lines. How to do it?
 3 Correct answers
3 Correct answers
I've written a script, based on maths I found (beyond my skills!) that draws the in-circle from three selected lines. (It can also draw the triangle made from the intersecting lines, but it's commented out for this post.)
/*
Make InCircle From Intersecting Lines.js
Draws a circle that fits inside the triangle made from three intersecting lines
(Also can draw the triangle made from intersection of lines)
by m1b (and vital contributors mentioned below!)
posted here: https://After selecting the three straight lines,
and "Divide" in Pathfinder,
all you have to do is drag the Live Corner to the center of the triangle.
I duplicated the triangle for illustration and used it as a guide.
Explore related tutorials & articles
Copy link to clipboard
Copied
You could convert the lines to guides and just move and scale the circle. If you have Astute's Collider Scribe as well this would be even easier...
Mylenium
Copy link to clipboard
Copied
Sorry, but can you please explain it with some images?
Copy link to clipboard
Copied
Copy link to clipboard
Copied
I do understand the geometry here, and thanks for sharing it. But, I want to know how to do it in illustrator.
Copy link to clipboard
Copied
Copy link to clipboard
Copied
Okkayy!! I've got to know how to do it now and I'm done with my work.
Just asking, is this the only way to do so, because I feel like we can do it more easily.
Copy link to clipboard
Copied
Some month/years ago, somebody ask the same question.
I didn't remember the users name, but somebody made a script for that.
Copy link to clipboard
Copied
Okkayy!! I've got to know how to do it now and I'm done with my work.
Just asking, is this the only way to do so, because I feel like we can do it more easily.
By @Nikxith
it's definitely not the only way of doing it, is it worth your time (or anyone else's) to find an easier way?
Copy link to clipboard
Copied
Sai Nikxith,
You can, Smart Guides being your friends, working on a copy of your three lines which are hidden beneath the copies:
1) Cut the lines at their intersections and delete the outer end parts so you work with a triangle, just keep them as separate lines;
2) In the stacking order (Layers panel) move the shortest line (lower rigth in your case) to the top if not already;
3) Click the top line to select it, then switch to the Rotate Tool, then Click one of the ends to set it as centre, then Alt/OptionClickDrag the other end to snap a copy to the other line from that corner, then delete the copy; now you have the full angle between the lines/sides;
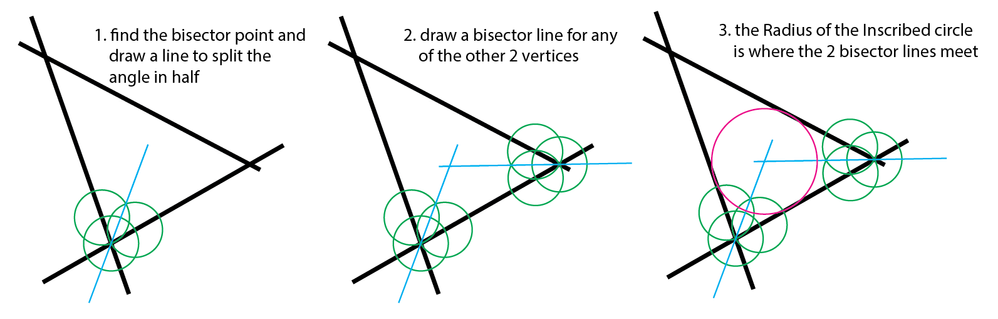
4) Alt/OptionClick the same corner, then divide the angle by 2 (just insert /2 in the box) and Copy; this is your first angle bisector;
5) Repeat 3) and 4), only at the other end; this is your second angle bisector, and their intersection is the centre of the incircle;
6) Switch to the the Selection Tool and click the top line, then copy it and rotate the copy by 90 degrees, then deselect and ClickDrag it by the relevant end Anchor Point to snap to the centre, then cut it at the intersection with the top line and delete the outer end part; now you have one normal with the radius of the incircle;
7) Select the normal and copy its length from the Document Info, then create a circle with twice the length as W=H (just add *2 in the first box);
8) ClickDrag the circle by its centre to snap to the centre from 5), and delete the unwanted bits.
Edit: I had to leave for (quite) a while before finishing.
Hi Carlos.
How about establishing the radius/diameter of the circle, so it can be created? I create/use a normal in 6) and 7).
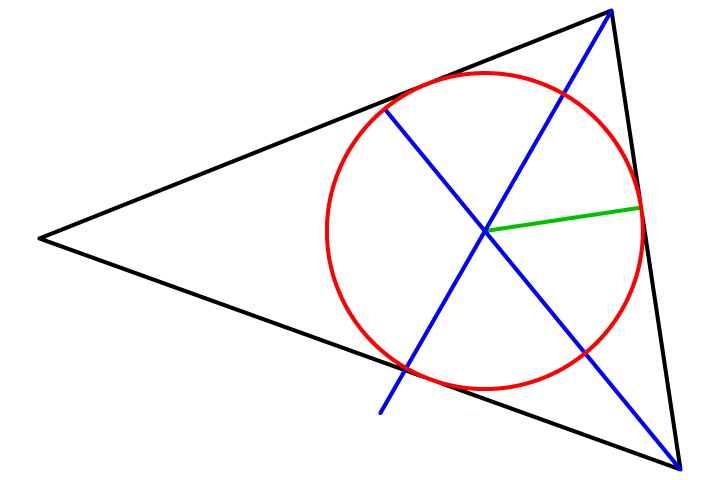
Edit edit: Here is a corresponding drawing, sides in black, angle bisectors in blue, normal in green, incircle in red; and I have improved the wording.
Copy link to clipboard
Copied
Hi Jacob, what about the radius/diameter? the value can be calculated mathematically, there's formula in the link I posted.
I didn't try your method yet but I'm sure it works.
Copy link to clipboard
Copied
Carlos,
Whenever I can, for all sorts of things, I leave the calculations to Illy and just draw, so I never thought of looking into the link for formulas; now I have seen the tough stuff.
Copy link to clipboard
Copied
🙂
Copy link to clipboard
Copied
Jacob, I set out to find another way to do this construction. I tried this way and that way, and finally, AHA! I had it!
I had very cleverly rebuilt your method.
Copy link to clipboard
Copied
Hi Peter.
Birds of a feather.
Copy link to clipboard
Copied
I've written a script, based on maths I found (beyond my skills!) that draws the in-circle from three selected lines. (It can also draw the triangle made from the intersecting lines, but it's commented out for this post.)
/*
Make InCircle From Intersecting Lines.js
Draws a circle that fits inside the triangle made from three intersecting lines
(Also can draw the triangle made from intersection of lines)
by m1b (and vital contributors mentioned below!)
posted here: https://community.adobe.com/t5/illustrator/three-tangent-circle/m-p/12204800
I found the mathematical code here:
https://dirask.com/posts/JavaScript-how-to-calculate-intersection-point-of-two-lines-for-given-4-points-VjvnAj
https://www.geeksforgeeks.org/program-to-find-the-incenter-of-a-triangle/
https://www.geeksforgeeks.org/program-to-find-the-radius-of-the-incircle-of-the-triangle/
Notes: not tested much and very little sanity checking!
*/
(function () {
// assume 3 line pathitems selected
// note the lines are treated as essentially infinite length,
// so they don't need to actually intersect
try {
if (selection.length != 3)
throw 'Please select three lines and try again.';
var line1 = selection[0];
var line2 = selection[1];
var line3 = selection[2];
if (!(itemIsLine(line1) && itemIsLine(line2) && itemIsLine(line3)))
throw 'Please select three lines and try again.'
// this makes a simple 'triangle' object of where the lines intersect
var myTriangle = triangleFromIntersectingLines(line1, line2, line3);
// this draws the triangle
// var myTrianglePathItem = makeTrianglePathItem(myTriangle);
// this draws the in-circle of the triangle
var myCirclePathItem = makeInCirclePathItem(myTriangle);
} catch (error) {
alert(error);
}
// functions
function triangleFromIntersectingLines(line1, line2, line3) {
var triangle = {};
triangle.points = [
pointOfIntersection(line1, line2),
pointOfIntersection(line2, line3),
pointOfIntersection(line3, line1)
];
triangle.sideLengths = [
distanceBetweenPoints(triangle.points[0], triangle.points[1]),
distanceBetweenPoints(triangle.points[1], triangle.points[2]),
distanceBetweenPoints(triangle.points[2], triangle.points[0])
];
return triangle;
}
function makeTrianglePathItem(triangle) {
var trianglePathItem = activeDocument.pathItems.add();
trianglePathItem.setEntirePath(new Array(
new Array(triangle.points[0][0], triangle.points[0][1]),
new Array(triangle.points[1][0], triangle.points[1][1]),
new Array(triangle.points[2][0], triangle.points[2][1])
));
trianglePathItem.closed = true;
return trianglePathItem;
}
function makeInCirclePathItem(triangle) {
// triangle is an object with points and sidelength properties
var circle = {};
circle.radius = radiusOfInCircle(triangle);
circle.center = calculateInCenter(triangle);
// make the in-circle
var circlePathItem = app.activeDocument.pathItems.ellipse(
circle.center[1] + circle.radius, // top
circle.center[0] - circle.radius, // left
circle.radius * 2, // width
circle.radius * 2 // height
)
return circlePathItem;
}
function pointOfIntersection(line1, line2) {
// line1 and line2 are expected to be PathItems with 2 PathPoints
if (line1 == undefined || line1.pathPoints == undefined || line1.pathPoints.length != 2)
throw "pointOfIntersection error: line1 doesn't have two points";
if (line2 == undefined || line2.pathPoints == undefined || line2.pathPoints.length != 2)
throw "pointOfIntersection error: line2 doesn't have two points";
var p1 = pointArrayToObject(line1.pathPoints[0].anchor),
p2 = pointArrayToObject(line1.pathPoints[1].anchor),
p3 = pointArrayToObject(line2.pathPoints[0].anchor),
p4 = pointArrayToObject(line2.pathPoints[1].anchor),
intersectionPoint = calculateIntersection(p1, p2, p3, p4);
return pointObjectToArray(intersectionPoint);
function pointArrayToObject(p) { return { x: p[0], y: p[1] } };
function pointObjectToArray(p) { return [p.x, p.y] };
}
function calculateIntersection(p1, p2, p3, p4) {
// p1, p2, p3 and p4 are expected to be objects with x and y values
// lower part of intersection point formula
var d1 = (p1.x - p2.x) * (p3.y - p4.y); // (x1 - x2) * (y3 - y4)
var d2 = (p1.y - p2.y) * (p3.x - p4.x); // (y1 - y2) * (x3 - x4)
var d = (d1) - (d2);
if (d == 0) throw 'Number of intersection points is zero or infinity.';
// upper part of intersection point formula
var u1 = (p1.x * p2.y - p1.y * p2.x); // (x1 * y2 - y1 * x2)
var u4 = (p3.x * p4.y - p3.y * p4.x); // (x3 * y4 - y3 * x4)
var u2x = p3.x - p4.x; // (x3 - x4)
var u3x = p1.x - p2.x; // (x1 - x2)
var u2y = p3.y - p4.y; // (y3 - y4)
var u3y = p1.y - p2.y; // (y1 - y2)
// intersection point formula
var px = (u1 * u2x - u3x * u4) / d;
var py = (u1 * u2y - u3y * u4) / d;
return { x: px, y: py };
}
function calculateInCenter(triangle) {
var x1 = triangle.points[0][0],
y1 = triangle.points[0][1],
x2 = triangle.points[1][0],
y2 = triangle.points[1][1],
x3 = triangle.points[2][0],
y3 = triangle.points[2][1],
a = triangle.sideLengths[1],
b = triangle.sideLengths[2],
c = triangle.sideLengths[0];
// Formula to calculate in-center
var x = (a * x1 + b * x2 + c * x3) / (a + b + c);
var y = (a * y1 + b * y2 + c * y3) / (a + b + c);
return [x, y];
}
function radiusOfInCircle(triangle) {
var a = triangle.sideLengths[0],
b = triangle.sideLengths[1],
c = triangle.sideLengths[2];
// the sides cannot be negative
if (a < 0 || b < 0 || c < 0)
return -1;
// semi-perimeter of the circle
var p = (a + b + c) / 2;
// area of the triangle
var area = Math.sqrt(p * (p - a) * (p - b) * (p - c));
// Radius of the incircle
var radius = area / p;
// Return the radius
return radius;
}
function distanceBetweenPoints(p1, p2) {
var a = p1[0] - p2[0];
var b = p1[1] - p2[1];
return Math.sqrt(a * a + b * b);
}
function itemIsLine(item) {
return item != undefined && item.pathPoints != undefined && item.pathPoints.length === 2;
}
})();
Copy link to clipboard
Copied
there you go, it couldn't get any easier for the OP
Copy link to clipboard
Copied
Carlos,
Actually, working on it yesterday I thought of scripting, and I wondered whether the drawn way I was using could form the basis of, or inspiration for, a script, or the two ways are (too) complementary.
I have sometimes pondered over that in other cases, and wondered what you would say.
Besides, when I saw your way, I was surpsised that you chose drawing rather than scripting.
But I was too entangled in urgencies yesterday to think of asking those questions.
Copy link to clipboard
Copied
Jacob, I always think of writing a script for complex queries, but writing scripts takes time I didn't have. Also the OP wanted to know how do it, so I thought showing how do it manually was what he needed.
Copy link to clipboard
Copied
Indeed, Carlos.
Copy link to clipboard
Copied
Can't be easier than this.
THANKS A LOTTT!!!
Copy link to clipboard
Copied
Your script is really beautiful, m1b.
Thanks for making and sharing it.
Copy link to clipboard
Copied
Thanks Kurt, I appreciate the generous comment. It was fun script to make. Of course the real beauty is in the maths, for which I take no credit. 🙂
Copy link to clipboard
Copied
Well, you have taken the right and the beautiful math, m1b.
Therefore I dare say that you provided the script of the year so far (let's see what will be there in the forthcoming months).
Copy link to clipboard
Copied
After selecting the three straight lines,
and "Divide" in Pathfinder,
all you have to do is drag the Live Corner to the center of the triangle.
I duplicated the triangle for illustration and used it as a guide.
-
- 1
- 2
Get ready! An upgraded Adobe Community experience is coming in January.
Learn more