Point coordinates on curved spline

[Tomas Sinkunas]

Hi guys.

I am banging my head to the wall for some time now with this issue.

As a simplified version, I have a perfect circle and I need to find midpoint coordinates between two vertices. In this case:

A is a vertex with coordinates [0, 0]

B is a vertex with coordinates [500, 0]

A1 is OutTangent of point A with coordinates [138, -138]

B1 is InTangent of point B with coordinates [362, -138]

The goal is to find midpoint coordinates.

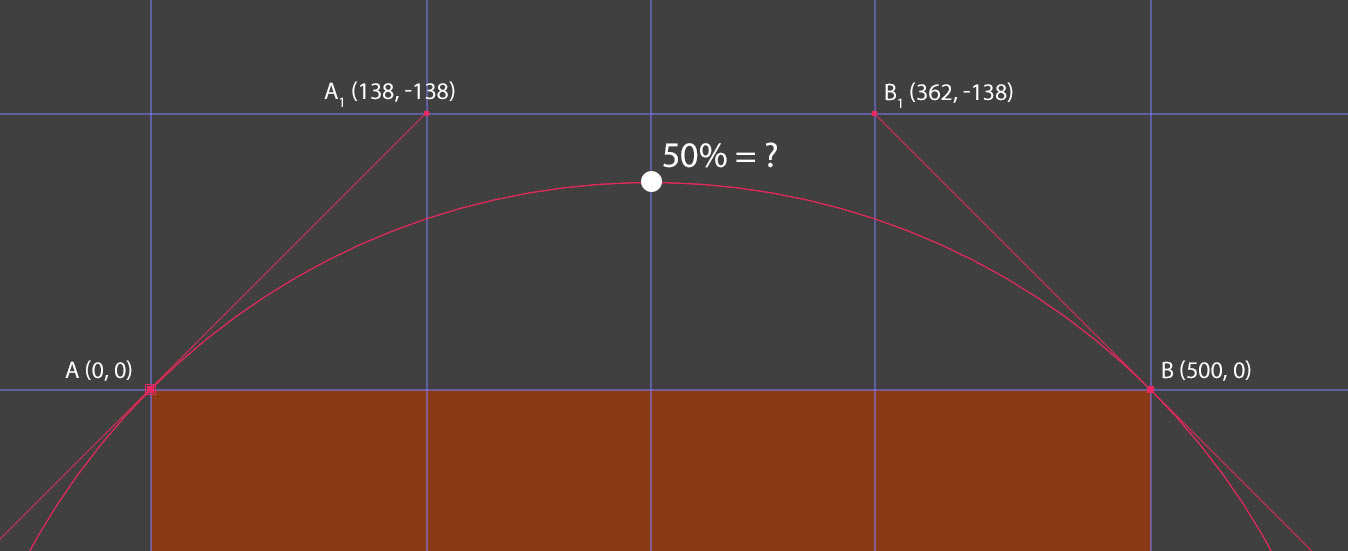
Again, this is very simple scenario. Other times tangent will be different lengths and shapes will be random as well, so I'd like to wrap my head around finding coordinates based on 2 vertices and InTangents and OutTangents.

Thanks in advance.

UQg‌,

[Mathias Moehl]

What about

1) compute the line that is perpendicular to the tangents of A

2) compute the line that is perpendicular to the tangents of B

3) the two lines from 1) and 2) intersect in exactly one point which is probably the point you are looking for

Before you think about how to implement this as a script, I recommend to think about whether this is exactly what you need. Because when you say you need the middle of a circle but also have very different shapes, a big question is what you actually want to compute exactly.

[Mathias Moehl]

oops, sorry, just noticed that I didn't understand you correctly. I thought you want to find the middle point of the circle, not the middle on the curve.

This video shows how individual points on a bezier curve are calculated

[Dan Ebberts · Accepted solution]

I think this works:

t = .5; // percentage along path (between 0 and 1)

p0 = [0,0]; // vertex 1

p1 = [138,-138]; // tangent 1

p2 = [362,-138]; // tangent 2

p3 = [500,0]; // vertex 2

c = 3*(p1 - p0);

b = 3*(p2 - p1) - c;

a = p3 - p0 - c - b;

((a*t +b )*t + c)*t + p0

Dan

[Tomas Sinkunas]

Dan, in case vertices don't have tangents (tangent values are [0, 0] for each vertex), the results looks off? Here's the values:

t = .25; // quater of the length

p0 = [0, 0]; // vertex 1

p1 = [0, 0]; // tangent 1

p2 = [100, 0]; // tangent 2

p3 = [100, 0]; // vertex 2

c = 3*(p1 - p0);

b = 3*(p2 - p1) - c;

a = p3 - p0 - c - b;

((a*t +b )*t + c)*t + p0 = [15.625, 0]

Shouldn't the result be [25, 0] (quarter of the spline length?)

[Dan Ebberts]

As I recall, the way the math works, for a straight line, the tangents need to be 1/3 of the way towards the other vertex. So [33.33333,0] and [66.66667,0] in your example.

Dan

[Tomas Sinkunas]

yeap, with [33.33333,0] and [66.66667,0] math is correct.

However, in AE vertex hard interpolation has tangents [0, 0]

[Dan Ebberts]

Maybe if both tangents are [0,0] you draw a line instead of a bezier?

Dan

[Tomas Sinkunas]

Mathias, that link you posted is exatly what I was trying to figure out. Thank for it.

And Dan, you are my hero. Your formula seems to work just perfect!!! Thank you.

How did you figure this out?

[Dan Ebberts]

I did the research a long time ago, back when I posted this:

Bezier Curve

I don't remember the original source docs.

Dan

[UQg]

Hi,

"old" thread but this might interest someone.

Normally calculating the point halfway on a bezier curve requires a numerical algorithm, a bunch of functions for it, and is subject to errors.

Here is a trick that let After Effects calculate things for you: it copies the path to a position property, makes sure that the speed is constant, and collect the mid points using valueAtTime("midTime").
Since it creates acomp and a layer, then removes it, it can be quite slow if used repetedly, but it's fine for one use:

function getMidPoints(shape){

    // collects the middle of each subcurve (bezier segment) in the shape;
    // returns these points (gathered into an array)
    // the number of mid points depends on the shape being closed or not.
    var ret = [];
    var v, i, o, N, NN, n, comp, p, t1, t2, x, t;
    // the parameter x can be set as an argument to allow other values
    x = 0.5;
    t1 = 0;
    t2 = 10;   
    t = x*(t2-t1);
    v = shape.vertices;
    i = shape.inTangents;
    o = shape.outTangents;
    N = v.length;
    NN = N-1;

    app.beginUndoGroup("Collect points");
    comp = app.project.items.addComp("temp", 10, 10, 1.0, 1.0, 1.0); // the comp spec don't matter
    p = comp.layers.addNull().transform.position;

    // shapes are 2D but a position property is 3D (optionnal for vertices, but mandatory for tangents, otherwise setSpatialTangentsAtKey will generate an error):
    for (n=0; n<N; n++){
        v[2] = 0;
        o[2] = 0;
        i[2] = 0;
        };

    // make sure that the temporal interpolation is LINEAR
    // in case that's not the default, do it now:
    p.addKey(t1); p.setInterpolationTypeAtKey(1, KeyframeInterpolationType.LINEAR, KeyframeInterpolationType.LINEAR);
    p.addKey(t2); p.setInterpolationTypeAtKey(2, KeyframeInterpolationType.LINEAR, KeyframeInterpolationType.LINEAR);

    for (n=0; n<NN; n++){
        p.setValuesAtTimes( [t1, t2], [v, v[n+1]]);
        // set spatial interpolation
        p.setSpatialTangentsAtKey(1, [0,0,0], o);
        p.setSpatialTangentsAtKey(2, i[n+1], [0,0,0]);
        // leave temporal interpolation to linear so that the null travels at constant speed
        ret.push(p.valueAtTime(t, true).slice(0,2));
        };
    if (shape.closed){
        p.setValuesAtTimes( [t1, t2], [v, v[0]]);
        p.setSpatialTangentsAtKey(1, [0,0,0], o);
        p.setSpatialTangentsAtKey(2, i[0], [0,0,0]);
        ret.push(p.valueAtTime(t, true).slice(0,2));
        };
    // delete everything;
    comp.layer(1).source.remove();
    comp.remove();
    app.endUndoGroup();

    return ret;
    };

function test(){
    // a mask must be selected
    // the test creates additionnal mask with just 1 vertex, one for each "midpoint"

    var comp = app.project.activeItem, props, p, points, n, N, L, shape;

    if (! (comp instanceof CompItem) || comp.selectedProperties.length===0) return;
    props = comp.selectedProperties;
    N = props.length;
    n=0; while (n<N && !props.isMask) ++n;
    if (n===N) {alert("Please select a mask"); return;};
    L = props.propertyGroup(2);
    points = getMidPoints(props.maskPath.value);
    N = points.length;
    for (n=0; n<N; n++){
        // Visualize points as shapes with just one vertex, on the same layer:
        shape = new Shape(); shape.vertices = [ points ];
        L.mask.addProperty("ADBE Mask Atom").maskPath.setValue(shape);
        };
    return;
    };

$.hiresTimer;
test();
alert($.hiresTimer);

Xavier.